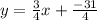Question

What is the slope-intercept form of the equation of a line that passes through (5, -4) and has a slope of `3/4`?

Answer 1

y = 3/4x -31/4

Explanation:

Answer 2

The slope-intercept form of the equation of a line that passes through (5, -4) and has a slope of `3/4 is
`y = (3)/(4)x + (-31)/(4)`

Solution:

Given that line passes through (5, -4)

Slope "m" =
`(3)/(4)`

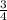
We have to find the slope intercept form

The slope intercept form is given as:

y = mx + b ---- eqn1

where "m" is the slope of the line and "b" is the y-intercept

Here in this sum m =
`(3)/(4)`

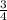
Calculating y-intercept:

Substitute (x, y) = (5, -4) and "m" value in eqn 1, we get

`\begin{array}{l}{-4=(3)/(4)(5)+b} \\\\ {-4=(15+4 b)/(4)} \\\\ {-16=15+4 b} \\\\ {4 b=-31} \\\\ {b=(-31)/(4)}\end{array}`

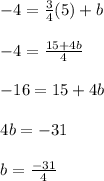
Now eqn 1 becomes,

`y = (3)/(4)x + (-31)/(4)`

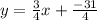
Hence the slope intercept form is
`y = (3)/(4)x + (-31)/(4)`