Question

What is the solution of the system x − 3y = –13 and 5x + 7y = 34? A. `x = (6)/(5)`, y = 4 B. `x = (7)/(2), y = (9)/(2)` C. `x = (1)/(2), y = (9)/(2)` D. x = –3, y = 7

Answer 1

C. X=1/2, Y=9/2

Explanation:

Answer 2

For this case we have the following system of equations:

`x-3y = -13\\5x + 7y = 34`

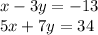
From the first equation we clear "x":

`x = -13 + 3y`

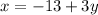
We substitute in the second equation:

`5 (-13 + 3y) + 7y = 34`

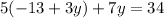
We apply distributive property:

`-65 + 15y + 7y = 34`

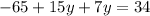
We add similar terms:

`-65 + 22y = 34`

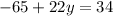
We add 65 to both sides:

`22y = 34 + 65\\22y = 99`

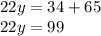
We divide between 22 on both sides:

`y = \frac {99} {22}\\y = \frac {9} {2}`

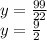
We look for the value of the variable "x":

`x = -13 + 3 \frac {9} {2}\\x = -13 + \frac {27} {2}\\x = \frac {-26 + 27} {2}\\x = \frac {1} {2}`

Thus, the solution of the system is:

`(x, y): (\frac {1} {2}, \frac {9} {2})`

ANswer:

`(x, y): (\frac {1} {2}, \frac {9} {2})`