Answer:
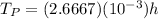
Step-by-step explanation:
Let's write the equation of the production rate for the assembly machine :
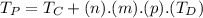
Where
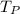 is the production rate for the assembly machine.
is the production rate for the assembly machine.
Where
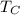 is the ideal cycle time
is the ideal cycle time
Where n is the number of stations.
Where m is the number stations that get jam when the defect occurs.
Where p is the defect rate at each station.
And where
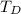 is the average downtime per breakdown
is the average downtime per breakdown
We are looking for the hourly production rate ⇒
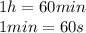 ⇒
⇒
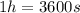 ⇒
⇒
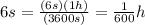
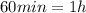 ⇒
⇒
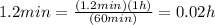
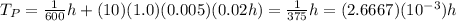
m = 1.0 in the equation.