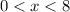Question

Write out the first few terms of the geometric​ series, Summation from n equals 0 to infinity (StartFraction x minus 4 Over 4 EndFraction )Superscript n ​, to find a and​ r, and find the sum of the series.​ Then, express the​ inequality, StartAbsoluteValue r EndAbsoluteValue less than 1​, in terms of x and find the values of x for which the inequality holds and the series converges.

Answer 1

a=1 converges for 0<x<8

Explanation:

Given that a geometric series infinite is given in summation form as

`\Sigma _0^\infty  ((x-4)/(4) )^n`

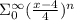
Here I term is when n =0

So a= I term =
`((x-4)/(4) )^0=1`

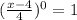
r = common ratio =
`(x-4)/(4)`

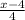
This series converges only if

`|r|<1`

`|(x-4)/(4)|<1\\-4<x-4<4\\0<x<8`

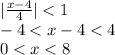
For 0<x<8, we get absolute value of r is less than 1.

Hence series converges for
`0<x<8`