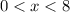Answer:
a=1 converges for 0<x<8
Explanation:
Given that a geometric series infinite is given in summation form as
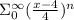
Here I term is when n =0
So a= I term =
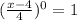
r = common ratio =
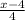
This series converges only if
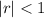
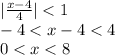
For 0<x<8, we get absolute value of r is less than 1.
Hence series converges for