Answer: B) 4
Step-by-step explanation:
I'm assuming you meant to say the interval
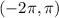
If so, then use your graphing calculator to look for the x intercepts, or roots, of y = x*cos(x) but only focus on the interval
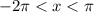
This is roughly from x = -6.28 to x = 3.14
You should find there are exactly four different roots on this interval. Each root of f '' (x) corresponds to a different point of inflection on f(x). Notice that the curve passes through the x axis for each root. Meaning that f '' (x) changes in sign as you pass through each root. A point of inflection is only possible if we have this sign change happening.