Question

The second derivative of a function is given by F"(x) = xcosx. How many points of inflection does f have on the interval (-2n, n)?

a)3 b)4 c)5 d)6

Answer 1

Answer: B) 4

Step-by-step explanation:

I'm assuming you meant to say the interval
`(-2\pi, \pi)`

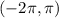
If so, then use your graphing calculator to look for the x intercepts, or roots, of y = x*cos(x) but only focus on the interval
`-2\pi < x < \pi`

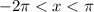
This is roughly from x = -6.28 to x = 3.14

You should find there are exactly four different roots on this interval. Each root of f '' (x) corresponds to a different point of inflection on f(x). Notice that the curve passes through the x axis for each root. Meaning that f '' (x) changes in sign as you pass through each root. A point of inflection is only possible if we have this sign change happening.