Answer:
From narrowest to widest:
1)
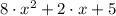
2)

3)
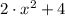
4)
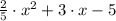
Explanation:
The "width" of the quadratic function is determined by the value of the coefficient associated by the monomial of highest grade, with respect to the primitive of the quadratic function, represented by
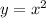 , whose ruling coefficient is 1. If the ruling coefficient of the quadratic function is greater than one, then the curve becomes narrower at the same time that the coefficient increases. Otherwise, if the ruling coefficient of the quadratic function is greater than zero and less than 1, then the curve becomes wider at the same time that the coefficient approximates to zero.
, whose ruling coefficient is 1. If the ruling coefficient of the quadratic function is greater than one, then the curve becomes narrower at the same time that the coefficient increases. Otherwise, if the ruling coefficient of the quadratic function is greater than zero and less than 1, then the curve becomes wider at the same time that the coefficient approximates to zero.
Based on this considerations, we proceed to list the quadratic functions from the narrowest to widest:
1)
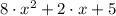
2)

3)
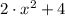
4)
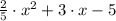
Lastly, we include a graphic with all polynomials (tagged as 1, 2, 3, 4) in comparison primitive function (tagged as 0).