Question

) There are 6.3 ✕ 1028 mobile electrons per cubic meter in tungsten. The cross-sectional area of the tungsten filament in bulb B1 is 0.01 mm2 (1 mm2 = 1 ✕ 10-6 m2). The electron mobility in hot tungsten is 1.2 ✕ 10-4 (m/s)/(N/C). Calculate the magnitude of the electric field inside the tungsten filament in bulb B1.

Answer 1

This is a typical ohm' law question on mobile electrons in an electric field E within a tungsten filament.

Recall that the drifting velocity u, of mobile electrons in this field can be expressed as

u = μ x E ........................ Eqn 1

where;

μ = mobility of electron carriers = 1.2 x 10⁻⁴ (m/s)/(N/C)

Recall, the Electric current I, number of electrons per second, can also be expressed as

I = n x A x u ........................ Eqn 2

Where I = 3 x 10¹⁸ e/s,

A = cross-sectional area of the filament wire = 1mm² = 1 x 10⁻⁶m²

n = no of electrons per unit volume = 6.3 x 10²⁸ e/m³

Substituting 'u' in Eqn 1 into Eqn 2 gives,

E =
`\frac{I}{{n}{A}{μ}}`

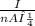
So, E =
`\frac{3 x 10¹⁸}{{6.3 x 10²⁸}{1 x 10⁻⁸}{1.2 x 10⁻⁴}}`

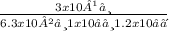
E = 39.7 N/C

Hence, the magnitude of the electric field inside the tungsten filament in bulb B1 is 39.7 N/C.