Answer:
This is a typical ohm' law question on mobile electrons in an electric field E within a tungsten filament.
Recall that the drifting velocity u, of mobile electrons in this field can be expressed as
u = μ x E ........................ Eqn 1
where;
μ = mobility of electron carriers = 1.2 x 10⁻⁴ (m/s)/(N/C)
Recall, the Electric current I, number of electrons per second, can also be expressed as
I = n x A x u ........................ Eqn 2
Where I = 3 x 10¹⁸ e/s,
A = cross-sectional area of the filament wire = 1mm² = 1 x 10⁻⁶m²
n = no of electrons per unit volume = 6.3 x 10²⁸ e/m³
Substituting 'u' in Eqn 1 into Eqn 2 gives,
E =
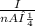
So, E =
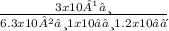
E = 39.7 N/C
Hence, the magnitude of the electric field inside the tungsten filament in bulb B1 is 39.7 N/C.