Answer:
F= 2.86KN
Step-by-step explanation:
The attached diagram shows the motion of crate on a single line The forces acting on it have been resolved as shown in the attached figure.The kinetic friction opposes the motion.Now crate is moving with constant speed so the acceleration is constant.
Applying Newton's second law to determine the force F and also substituting the values for
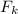 to eliminate normal force
to eliminate normal force
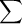 F = ma
F = ma
Now
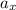 and
and
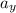 components are zero
components are zero
Horizontal and vertical forces are Force on crate, weight of crate and kinetic friction

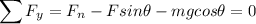
therefore

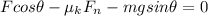 >>> (1)
>>> (1)
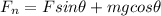
By putting the above equation in equation 1 we get F
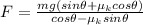
By putting values we get
F =
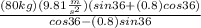
F= 2860.8 N
F= 2.86KN