Question

Suppose you start with a full tank of gas (15 gallons) in your truck. After driving 4 hours, you now have 6 gallons left. If x is the number of hours you have been driving, then y is the number of gallons left in the tank. At what rate is your truck using gas? State your answer as a reduced fraction.

Answer 1

`2(1)/(4) gallon per hour`

Explanation:

The rate at which the truck will consume gas depends on some factors which include:

1. Environmental factors (Weather)
2. Average Speed
3. Weight of the truck
4. Congestion
5. Driving behaviour of the driver.

Assuming all the conditions are uniform throughout the journey, then,

the rate at which the truck is using gas =
`(Total gas used)/(Time taken)`

Time taken = The number of hours you have been driving = x

x = 4 hours

Total gas used = Volume of gas in the tank at start - Volume of gas left in the tank

Total gas used = 15 gallons - y

Total gas used = 15 gallons - 6 gallons

Total gas used = 9 gallons

The rate at which the truck is using gas =
`(9 gallons)/(4 hours)`

=
`(9)/(4) gallon per hour`

=
`2(1)/(4) gallon per hour` (reduced fraction)

Answer 2

The rate is 2 1/4 gallons per hour

Explanation:

Let

x -----> the number of hours you have been driving

y ----> the number of gallons left in the tank

we know that

The linear equation in slope intercept form is equal to

`y=mx+b`

where

m is the unit rate or the slope

b is the y-intercept or initial value (value of y when the value of x is equal to zero)

In this problem we have the points

(0,15) and (4,6)

Find the slope

The formula to calculate the slope between two points is equal to

`m=(y2-y1)/(x2-x1)`

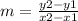
substitute the given values

`m=(6-15)/(4-0)`

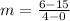
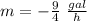`m=-(9)/(4)\ (gal)/(h)` ----> is negative because is a decreasing function

Convert to mixed number

`(9)/(4)\ (gal)/(h)=(8)/(4)+(1)/(4)=2(1)/(4)\ (gal)/(h)`

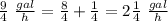
therefore

The rate is 2 1/4 gallons per hour