Question

ABC has A(-3,6),B(2,1),and C(9,5) as its vertices the length of side AB is 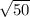units . The length of side BC is 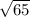?units . The length of side AC is ? Units .ABC ?

Answer 1

The length of side AB is
`√(50)` units.

The length of side BC is
`√(65)` units.

The length of side AC is
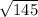`√(145)` units.

Explanation:

To find the length of each side, we use the formula for the distance between two points.

Distance between two points:

Points
`(x_1,y_1)` and
`(x_2,y_2)`. The distance between them is given by:

`D = √((x_2-x_1)^2+(y_2-y_1)^2)`

Side AB:

Points
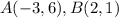`A(-3,6),B(2,1)`. So the distance between them is:

`D = √((2-(-3))^2 + (1-6)^2) = √(50)`

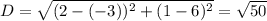
The length of side AB is
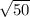`√(50)` units.

Side BC:

Points
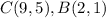`C(9,5),B(2,1)`. So the distance between them is:

`D = √((2-9)^2 + (1-5)^2) = √(65)`

The length of side BC is
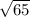`√(65)` units.

Side AC:

Points
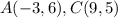`A(-3,6),C(9,5)`. So the distance between them is:

`D = √((9-(-3))^2 + (5-6)^2) = √(145)`

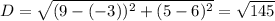
The length of side AC is
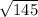`√(145)` units.