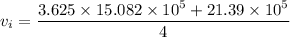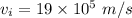Question

An alpha particle collides with an oxygen nucleus, initially at rest. The alpha particle is scattered at an angle of 25.0° above its initial direction of motion, and the oxygen nucleus recoils at an angle of 50.0° below this initial direction. The final speed of the oxygen nucleus is 2.08×105 m/s. (The mass of an alpha particle is 4.0 u, and the mass of an oxygen nucleus is 16 u.) What is the final speed of the alpha particle?

Answer 1

`v_(i)= 19* 10^5\ m/s`

Step-by-step explanation:

given,

scattering angle of alpha particle = 25.0° above its initial direction of motion

oxygen nucleus recoils at = 50.0° below this initial direction.

final speed of the oxygen = 2.08×10⁵ m/s

mass of alpha particle = 4.0 u

mass o oxygen nucleus = 16 u

momentum conservation along x- axis

`m_(a)v_(i) = m_a v_a cos\theta + m_o v_o cos\theta`

`4v_(i) = 4* v_a cos25^0 + 16* 2.08 * 10^5 cos50^0`

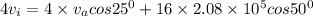
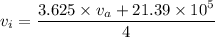`v_(i)= (3.625* v_a+ 21.39* 10^5)/(4)`....(1)

Along y-direction

`0 = m_av_a sin \theta - m_ov_o sin\theta`

`0 = 4* v_a sin 25 - 16*  2.08 * 10^5 sin50^0`

`v_a = (25.49 * 10^5)/(1.69)`

`v_a = 15.082* 10^5\ m/s`

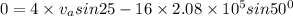
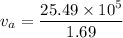
putting value in equation (1)

`v_(i)= (3.625* 15.082* 10^5+ 21.39* 10^5)/(4)`

`v_(i)= 19* 10^5\ m/s`