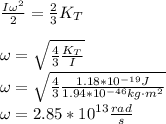Answer:
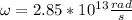
Step-by-step explanation:
The translational kinetic energy depends on the mass and speed of the body, as follows:
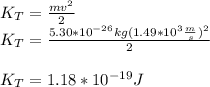
While rotational kinetic energy depends on the moment of inertia and the angular velocity of the body, as follows:
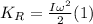 . We know that:
. We know that:
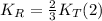
Replacing (1) in (2):