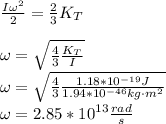Question

The oxygen molecule, O2, has a total mass of 5.30×10-26 kg and a rotational inertia of 1.94×10-46 kg-m2 about an axis perpendicular to the center of the line joining the atoms. Suppose that such a molecule in a gas has a speed of 1.49×103 m/s and that its rotational kinetic energy is two-thirds (2/3) of its translational kinetic energy.

What then is the molecule's angular speed aboutthe center of mass. (rad/s)

Answer 1

`\omega=2.85*10^(13)(rad)/(s)`

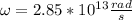
Step-by-step explanation:

The translational kinetic energy depends on the mass and speed of the body, as follows:

`K_T=(mv^2)/(2)\\K_T=(5.30*10^(-26)kg(1.49*10^3(m)/(s))^2)/(2)\\\\K_T=1.18*10^(-19)J`

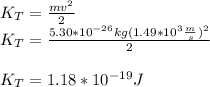
While rotational kinetic energy depends on the moment of inertia and the angular velocity of the body, as follows:

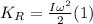`K_R=(I\omega^2)/(2)(1)`. We know that:

`K_R=(2)/(3)K_T(2)`

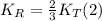
Replacing (1) in (2):

`(I\omega^2)/(2)=(2)/(3)K_T\\\\\omega=\sqrt{(4)/(3)(K_T)/(I)}\\\omega=\sqrt{(4)/(3)(1.18*10^(-19)J)/(1.94*10^(-46)kg\cdot m^2)}\\\omega=2.85*10^(13)(rad)/(s)`