The point-slope form and standard form of (3,1) and (4, 2) are y – 1 = x – 3 and x – y = 2 respectively
Solution:
Given, two points are (3, 1) and (4, 2)
We have to find that a line that passes through the given two points.
First let us find the slope of the line that passes through given two points.
Slope of line "m" is given as:
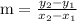


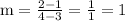
The point slope form is given as:
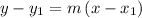
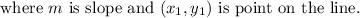
y – 1 = 1(x – 3)
y - 1 = x - 3
Line equation in point slope form is y – 1 = x – 3 -- eqn 1
Now, line equation in standard form i.e. ax + by = c is found out by eqn 1
y – 1 = x – 3
x – y = 3 – 1
x – y = 2
Hence, the line equation in point slope form and standard forms are y – 1 = x – 3 and x – y = 2 respectively