Answer:
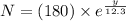 mg
mg
Step-by-step explanation:
For radioactive decay of an radioactive isotope-

Where N is amount of radioactive isotope after "t" time,
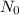 is initial amount of radioactive isotope and
is initial amount of radioactive isotope and
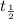 is half-life of radioactive isotope
is half-life of radioactive isotope
Here,
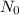 = 180 mg,
= 180 mg,
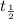 = 12.3 years, t = y years
= 12.3 years, t = y years
So,
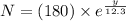 mg
mg
The above expression gives the remaining quantity of tritium after y years