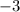Question

A line with a slope id -1/2 passes through the points (3,-1) and (p,2). what is the value of p

Answer 1

The value of p is -3 for the line that passes through (3, -1) and (p, 2)

Solution:

Given, two points are (3, -1) and (p, 2) and slope is
`(-1)/(2)`

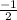
We have to find the value of p

Slope of a line that passing through
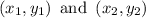`\left(x_(1), y_(1)\right) \text { and }\left(x_(2), y_(2)\right)` is given as:

`\mathrm{m}=(y_(2)-y_(1))/(x_(2)-x_(1))`

`\text { Here, in our problem, } x_(1)=3, y_(1)=-1 \text { and } x_(2)=p, y_(2)=2`

`\text { slope } m=(2-(-1))/(p-3)=(2+1)/(p-3)=(3)/(p-3)`

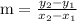
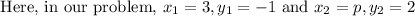
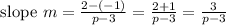
And, according to given information, slope value is given

`\begin{array}{l}{(3)/(p-3)=-(1)/(2)} \\\\ {-1(p-3)=3 * 2} \\\\ {-p+3=6} \\\\ {p=3-6} \\\\ {p=-3}\end{array}`

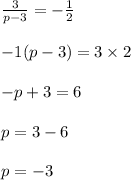
Hence, the value of p is
`-3`