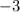The value of p is -3 for the line that passes through (3, -1) and (p, 2)
Solution:
Given, two points are (3, -1) and (p, 2) and slope is
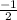
We have to find the value of p
Slope of a line that passing through
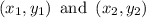 is given as:
is given as:
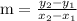
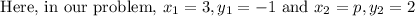
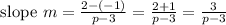
And, according to given information, slope value is given
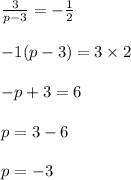
Hence, the value of p is