Question

The equation below expresses the approximate

height h, in meters, of a ball t seconds after it is
launched vertically upward from the ground.
h(t) = –16t2 + 25t. At how many different times will the ball be 7 ft. High?

Answer 1

The ball will be the 7 ft high at 2 different times.

Explanation:

The height in meters of the ball is given by the following equation:

`h(t) = -16t^2 + 25t`

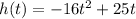
7 feet high

The height, by the equation, is given in meters, so we have to work in meters. Since each feet has 0,3048 meters, 7 feet have have 2.1336 meters. So, we have to solve the following equation

`2,1336 = -16t^2 + 25t`

`16t^2 - 25t + 2,1336 = 0`

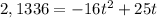
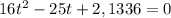
At how many different times will the ball be 7 ft. High?

We have to find the number of solutions for the equation above.

It is given according to the value of
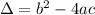`\Delta = b^2 - 4ac`. If it is positive, there are two solutions, zero one solution and negative no solutions.

In this equation
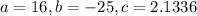`a = 16, b = -25, c = 2.1336`. So

`\Delta = b^2 - 4ac = (-25)^2 - 4*16*2.1336 = 488`

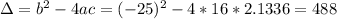
Since the coefficient is positive, the ball will be the 7 ft high at 2 different times.