Question

The length of EF in the right triangle

Answer 1

F.

`√(217)`

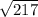
Explanation:

Use the Pythagorean Theorem, which is a^2 + b^2 = c^2.

c represents the hypotenuse, or the longest side of the right triangle. c in this case would be 19.

Side a can be represented as 12 since it is the other side that has a given value.

Substitute in the values to get the equation: (12)^2 + b^2 = (19)^2

12 squared is 144 and 19 squared is 361. To figure out what b^2 is subtract 361 - 144 to isolate the variable. We will be left with b^2 = 217.

In order to find what b is, find the square root of 217, which is Choice F.

Answer 2

In order to find the sides of a right triangle, you can use the pythagorean theorem. (a^2 + b^2 = c^2)

The pythagorean theorem basically means that the square of two sides is equal to the square of the hypotenuse (the longest side of a triangle)

In this case, we already have 'a' and 'c', but not 'b'.

12^2 + b^2 = 19^2

Mutliply everything:

144 + b^2 = 361

Isolate b into one side by subtracting both sides by 144:

b^2 = 217

Square root both sides in order to completely isolate b:

b =
`√(217)`

The answer is Option F

Good luck!