Question

6. A rotation maps a triangle with vertices A(3,1), B(-1,-1), and C(7,-2) to 4 A'B'C". What is the

length of B'C', to the nearest unit?

A) 4

B) 5

C) 8

D) 9

Answer 1

Option C.

Explanation:

It is given that a rotation maps a triangle with vertices A(3,1), B(-1,-1), and C(7,-2) to A'B'C'.

We know that rotation is a rigid transformation. It means the size and shape of the figure remains same. In other words we can say that preimage and image are congruent.

`\triangle ABC\cong \triangle A'B'C'`

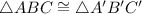
The corresponding parts of congruent triangles are congruent.

`BC\cong B'C'`

`BC=B'C'`

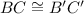
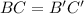
Distance formula:

`D=√((x_2-x_1)^2+(y_2-y_1)^2)`

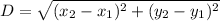
The distance of B(-1,-1), and C(7,-2) is

`BC=√((7-(-1))^2+(-2-(-1))^2)`

`BC=√((8)^2+(1)^2)`

`BC=√(65)`

`BC\approx 8.06`

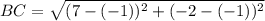
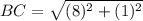
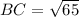
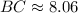
Approx to the nearest unit.

`BC=B'C'=8`

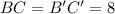
Therefore, the correct option is C.