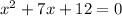Answer:
x = -3, or x = -4 is the solution for the given algebraic expression
Explanation:
Here, the given algebraic equation is:
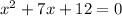
Now, solving this expression by splitting the middle term, we get
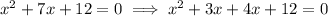
⇒ x ( x+3) + x (x+3) = 0
⇒(x+3) (x+4) = 0
⇒ either (x+3) = 0, or (x+4) = 0
Hence, either x = - 3, or x = - 4
Hence, x = -3, or x = -4 is the solution for the given algebraic expression