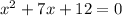Question

X^2+7x+12=0
Algebraic proofs
Solve each equation, write a reason for every step.

Answer 1

x = -3, or x = -4 is the solution for the given algebraic expression
`x^(2)  + 7x + 12 = 0`

Explanation:

Here, the given algebraic equation is:

`x^(2)  + 7x + 12 = 0`

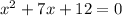
Now, solving this expression by splitting the middle term, we get

`x^(2)  + 7x + 12 = 0   \implies x^(2)  + 3x + 4x + 12 = 0`

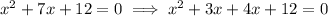
⇒ x ( x+3) + x (x+3) = 0

⇒(x+3) (x+4) = 0

⇒ either (x+3) = 0, or (x+4) = 0

Hence, either x = - 3, or x = - 4

Hence, x = -3, or x = -4 is the solution for the given algebraic expression
`x^(2)  + 7x + 12 = 0`