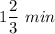Answer: The expected waiting time is
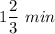
Explanation:
Since we have given that
Average waiting time for slow elevator = 3 min
Average waiting time for fast elevator = 1 min
probability that a person choose the fast elevator =

Probability that a person choose the slow elevator =

So, the expected waiting time would be
![E[x]=\sum xp(x)=3* (1)/(3)+1* (2)/(3)\\\\=1+(2)/(3)\\\\=(3+2)/(3)\\\\=(5)/(3)\\\\=1(2)/(3)\ min](https://img.qammunity.org/2020/formulas/mathematics/college/ly81ydtnozijm5vixpzagilau4ruilcowi.png)
Hence, the expected waiting time is