Question

A container of gas molecules is at a pressure of 2 atm and has amass density of 1.7 grams per liter. All of the molecules in thecontainer are diatomic nitrogen molecules with an atomic weight of28 grams per mole. What is the typical speed of the nitrogenmolecules in the container? Here we define the typical speed to bethe root-mean-square velocity (RMS velocity = vrms) ofthe center of mass of the molecule

Answer 1

The speed of nitrogen molecule is 1.87 m/s.

Step-by-step explanation:

Given that,

Pressure = 2 atm

Density = 1.7 grams/liter

Atomic weight = 28 grams

We need to calculate the temperature

Using formula of idea gas

`PV=nRT`

`P=(WRT)/(VM)`

`P=(\rho RT)/(M)`

`T=(PM)/(\rho R)`

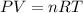
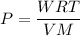
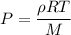
Put the value into the formula

`T=(2*28)/(1.7*0.0821)`

`T=401.2\ K`

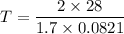
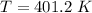
We need to calculate the speed of nitrogen molecule

Using formula of RMS speed

`V_(rms)=\sqrt{(3RT)/(M)}`

`V_(rms)=\sqrt{(3*0.0821*401.2)/(28)}`

`V_(rms)=1.87\ m/s`

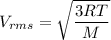
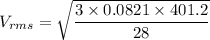
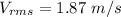
Hence, The speed of nitrogen molecule is 1.87 m/s.