Answer:
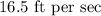
Explanation:
Let the length of rope is x and y be the distance of the balloon from the ground,
Given,
The spool of rope that is 125 feet away from the balloon,
By making the diagram of this scenario,
Using Pythagoras theorem,
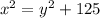
Differentiating with respect to time (t),
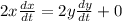
We have,
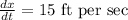
If time = 20 seconds,
So, x = 15 × 20 = 300 ft ( ∵ distance = speed × time )
By substituting the values,
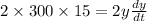
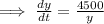
Since,
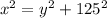 and x = 300 ft,
and x = 300 ft,
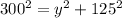
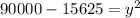
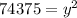
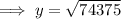
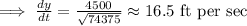
Hence, the hot air balloon is rising with the speed of 16.5 ft per sec.