Question

A gas flows along the x axis with a speed of V = 5x m/s and a pressure of p = 10x2 N/m2 , where x is in meters.

(a) Determine the time rate of change of pressure at the fixed location x = 1 (i.e., for the particle currently at x=1).

(b) Determine the time rate of change of pressure for a fluid particle flowing past x = 1. (you are fixed at x=1)

(c) Explain without using any equations why the answers to parts (a) and (b) are different.

Answer 1

Step-by-step explanation:

Given that,

Speed = 5x m/s

Pressure = 10x² N/m²

(a). We need to calculate the time rate of change of pressure at the fixed location x = 1

Using formula of rate of change of pressure at fixed location

`(\delta P)/(\delta t)=(\delta)/(\delta t)(10x^2)`

`(\delta P)/(\delta t)=0`

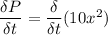
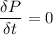
(b). We need to calculate the the time rate of change of pressure for a fluid particle flowing past x = 1

Using formula of rate of change of pressure at the given instant

`(DP)/(Dt)=(\delta P)/(\delta t)+u(\delta P)/(\delta x)+(\delta P)/(delta y)+(\delta P)/(\delta z)`

`(DP)/(Dt)=u(\delta P)/(\delta x)`

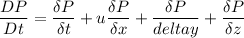
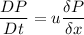
Put the value into the formula

`(DP)/(Dt)=5x(\delta)/(\delta x)(10x^2)`

`(DP)/(Dt)=5x*20x`

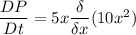
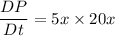
At x = 1,

`(DP)/(Dt)=100\ N/m^2 s`

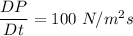
(c). The velocity is instantaneous at x = 1 for a part and for b part the velocity is steady flow.

Therefore, the answer is different for a and b part.

Hence, This is the required solution.