Step-by-step explanation:
Given that,
Speed = 5x m/s
Pressure = 10x² N/m²
(a). We need to calculate the time rate of change of pressure at the fixed location x = 1
Using formula of rate of change of pressure at fixed location
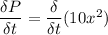
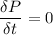
(b). We need to calculate the the time rate of change of pressure for a fluid particle flowing past x = 1
Using formula of rate of change of pressure at the given instant
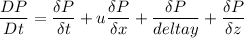
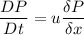
Put the value into the formula
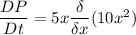
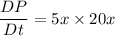
At x = 1,
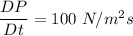
(c). The velocity is instantaneous at x = 1 for a part and for b part the velocity is steady flow.
Therefore, the answer is different for a and b part.
Hence, This is the required solution.