Question

Assume that a manhole is constructed to have a circular opening with a diameter of 22 in. Men have shoulder breadths that are normally distributed with a mean of 18.2 in and a standard deviation of 1.0 in. a. Assume that the Connecticut Light and Power company employs 36 men who work in manholes. If 36 men are randomly selected, what is the probability that their mean shoulder breadth is less than 18.5 in? Does this result suggest that money can be saved by making smaller manholes with a diameter of 18.5 in? Why or why not

Answer 1

0.964 is the probability that their mean shoulder breadth is less than 18.5 inch.

Explanation:

Given:

Mean, μ = 18.2 inch

Standard Deviation, σ = 1.0 inch

n = 36

We are given that the distribution of shoulder breadths is a bell shaped distribution that is a normal distribution.

Formula:

`z_(score) = \displaystyle(x-\mu)/((\sigma)/(√(n)))`

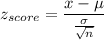
a) P( mean shoulder breadth is less than 18.5 inch)

P(x < 18.5)

`P( x < 18.5) = P( z < \displaystyle(18.5-18.2)/((1)/(√(36)))) = P(z < 1.8)`

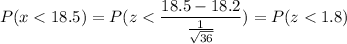
Calculation the value from standard normal z table, we have,

`P(x < 18.5) =0.964= 96.4\%`

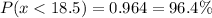
Thus, 0.964 is the probability that their mean shoulder breadth is less than 18.5 inch.

Yes, the result suggest that money can be saved by making smaller manholes with a diameter of 18.5 inch since 96.4% of the man holes have their mean shoulder breadth less than 18.5 inch.