Question

The population of a colony of mosquitoes obeys the law of uninhibited growth. If there are 1000 mosquitoes initially and there are 1900 after 1 day, what is the size of the colony after 4 days? How long is it until there are 60,000 mosquitoes? What is the size of the colony after 4 days? mosquitoes (Round to the nearest whole number.) How long is it until 60,000 mosquitoes are in the colony? days (Round to the nearest tenth.)

Answer 1

24761 mosquitoes

5.4 days

Explanation:

Let the equation that shows the population of the mosquitoes after x days,

`A=P(1+r)^x`

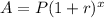
Where,

P = Initial population,

r = rate of increasing per day,

Here, A = 1000, when x = 0,

`1000=P(1+r)^0\implies P = 1000`

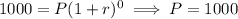
A = 1900 when x = 1,

`1900 = P(1+r)^1\implies 1900 = 1000(1+r)\implies 1.9 = 1 + r\implies r = 0.9`

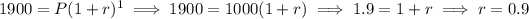
Thus, the required function that represents the population after x days,

`A=1900(1+0.9)^x=1900(1.9)^x`

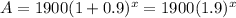
If x = 4,

The number of mosquito after 4 days,

`A=1900(1.9)^4 = 24760.99\approx 24761`

If A = 60,000,

`60000 = 1900(1.9)^x`

`(600)/(19)=1.9^x`

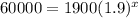
Taking log both sides,

`\log((600)/(19))=x\log 1.9`

`\implies x = (\log((600)/(19)))/(\log 1.9)=5.378\approx 5.4`

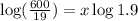
Thus, there will 60,000 mosquitoes after 5 days.