Question

Which system of equations has the same solution as the system below?

3x + 3y = 8
2x - y = 5

Answer 1

x = 23/9 y = .11

Explanation:

We can solve for the systems of equation by elimination.

Multiply the second equation by 3.

6x - 3y = 15

3x + 3y = 8

9x = 23

x = 23/9

Answer 2

B. 3x + 3y = 8 and 4x - 2y = 10 has the same solution as 3x+3y=8 and 2x-y=5

Why is this correct?

Two systems are considered to have the same solution if solving each system leads to identical values for x and y.

Analyzing the given options;

A.
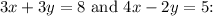`\(3x + 3y = 8\) and \(4x - 2y = 5\):` The first equation remains the same, but the second equation has a different constant term (5 instead of 10). This results in a distinct solution for y, making this option incorrect.

B.
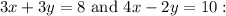`\(3x + 3y = 8\) and \(4x - 2y = 10: \)` This option alters the second equation by multiplying both sides by 2. Consequently, the constant term becomes 10, yet the coefficients of x and y remain proportional to those in the original second equation. Solving this system will yield the same values for x and y as the original system, making this the correct answer.

C.
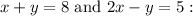`\(x + y = 8\) and \(2x - y = 5: \)` This option changes the first equation by multiplying both sides by 3. This modification leads to a different value for y, rendering this option incorrect.

D.
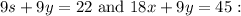`\(9s + 9y = 22\) and \(18x + 9y = 45: \)` These equations include different variables (s instead of x) and constants, making them unrelated to the original system.

Therefore, only option B,
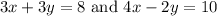`\(3x + 3y = 8\) and \(4x - 2y = 10\)`, aligns with the given system and has the same solution.

Complete question:

Which system of equations has the same solution as the system below? 3x+3y=8 2x-y=5 A. 3x+3y=8 4x-2y=5 B. 3x+3y=8 4x-2y=10 C. x+y=8 2x-y=5 D. 9s+9y=22 18x+9y=45