Question

Given square ABCD with diagonals AC, BD.
If DB = 7x + 1 and AE = 2x + 11, find EB.

Answer 1

The length of EB is 25 unit

Explanation:

Given as:

ABCD is a square With diagonal AC and BD

The length of DB = 7x + 1

The length of AE = 2x + 11

The mid point of BD and AC is E

Let the each side of square be m

So, BD² = m² + m²

Or, (7x + 1) = 2 m²

Or m² =
`((7x + 1))/(2)`

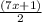
Again

AC² = m² + m² = 2 m²

Or, AC = (7x + 1)

∵ AE is the half of diagonal AC

So, AE =
`(1)/(2)` × (7x + 1)

Or, 2x + 11 =
`(1)/(2)` × (7x + 1)

or , 4x + 22 = 7x + 1

Or, 3x = 21

∴ x = 7 unit

So, BD = 7 (7 ) + 1 = 50 unit

So, BE is the half of diagonal BD

Or, BE =
`(1)/(2)` × 50 = 25 unit

Hence The length of EB is 25 unit Answer