Question

If Triangle PQR ~ Triangle SQT, Find the value of x.

Answer 1

x = 15

Explanation:

x+13/9 = 21/x-9

x^2+4x−117=168

x^2+4x−285=0

(x−15)(x+19)=0

x=15

it cannot be a negative number so x cannot be -19

Answer 2

x = 15

Explanation:

Given that ∆PQR ~ ∆SQT, therefore their side lengths are proportional to each other.

Thus:

`(PQ)/(SQ) = (PR)/(ST)`

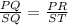
PQ = (x + 5) + 8 = x + 13

SQ = 8

PR = 21

ST = x - 9

Plug in the values

`(x + 13)/(8) = (21)/(x - 9)`

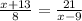
Cross multiply

`(x + 13)(x - 9) = 8*21`

`x(x - 9) +13(x - 9) = 168`

`x^2 - 9x + 13x - 117 = 168`

`x^2 + 4x - 117 = 168`

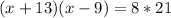
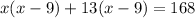
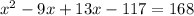
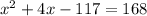
Subtract 168 from both sides

`x^2 + 4x - 117 - 168 = 0`

`x^2 + 4x - 285 = 0`

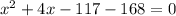
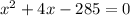
Factorize

`x^2 + 19x - 15x - 285 = 0`

`x(x + 19) - 15(x + 19) = 0`

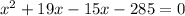
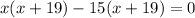
(x + 19)(x - 15) = 0

x = -19 or x = 15