Answer:
x = 15
Explanation:
Given that ∆PQR ~ ∆SQT, therefore their side lengths are proportional to each other.
Thus:
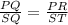
PQ = (x + 5) + 8 = x + 13
SQ = 8
PR = 21
ST = x - 9
Plug in the values
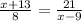
Cross multiply
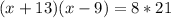
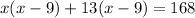

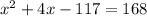
Subtract 168 from both sides
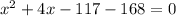

Factorize
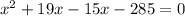

(x + 19)(x - 15) = 0
x = -19 or x = 15