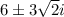Question

Solve for x in the equation X2-12x+36 = 90

Answer 1

The value of "x" in x^2 -12x + 36 = 90 is
`6 \pm 3 √(2) i`

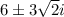
Solution:

Given, equation is
`x^(2)-12 x+36=90`

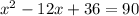
We have to solve the above given equation for the "x" value

Now, take the given equation,

`\begin{array}{l}{\rightarrow x^(2)-12 x+36=90} \\\\ {\rightarrow x^(2)-12 x+36-90=0} \\\\ {\rightarrow x^(2)-12 x+54=0}\end{array}`

Now, let us use the quadratic formula

`\mathrm{x}=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`

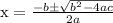
Here a = 1, b = -12, c = 54

`\begin{array}{l}{x=\frac{-(-12) \pm \sqrt{(-12)^(2)-4 * 1 * 54}}{2 * 1}} \\\\ {x=(12 \pm √(144-216))/(2)} \\\\ {x=(12 \pm √(-72))/(2)} \\\\ {x=(12 \pm √(72) * √(-1))/(2)} \\\\ {x=(12 \pm 6 √(2) i)/(2)} \\\\ {x=6 \pm 3 √(2) i}\end{array}`

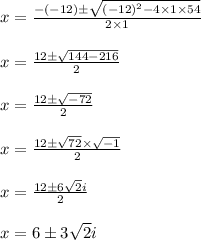
Hence, the value of "x" is
`6 \pm 3 √(2) i`