Question

Situation A bichromatic source produces light having wavelengths in vacuum of 450 nm and 650 nm. The indices of refraction are 1.440 and 1.420, respectively. In the situation above, a ray of the bichromatic light, in air, is incident upon the oil at an angle of incidence of 50.0°. The angle of dispersion between the two refracted rays in the oil is closest to:

Answer 1

`\theta=0.52^(\circ)`

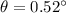
Step-by-step explanation:

It is given that,

Wavelength in vacuum,
`\lambda_1=450\ nm`

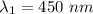
Wavelength in vacuum,
`\lambda_2=650\ nm`

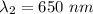
Refractive index for air,
`n_1=1`

First refractive index,
`n =1.44`

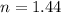
Second refractive index,
`n' =1.42`

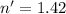
A ray is incident at an angle of incidence of 50 degrees. Let r is the angle of refraction. Firstly calculating the angle of refraction for two values of wavelength from Snell's law as :

`(sin\ i)/(sin\ r)=(n_2)/(n_1)`

`r=sin^(-1)((n_1\ sin\ i)/(n))`

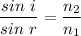
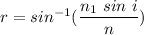
For 450 nm,
`r=sin^(-1)((1\ sin(50))/(1.44))`

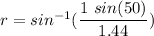
r = 32.13 degrees

For 650 nm,
`r'=sin^(-1)((1\ sin(50))/(1.42))`

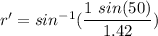
r' = 32.65 degrees

Let
`\theta` is the angle of dispersion between the two refracted rays in the oil such that,

`\theta=r'-r`

`\theta=32.65-32.13`

`\theta=0.52^(\circ)`

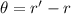
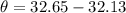
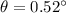
So, the angle of dispersion between the two refracted rays in the oil is closest to 0.52 degrees.