Question

Solve system with substitution

Julia and Willie each improved their yard by planting rose bushes and shrubs. They bought their supplies from the same store. Julia spent $136 on 11 rose bushes and 4 shrubs. Willie spent $148 on 2 rose bushes and 11 shrubs. Find the cost of one rose bush and the cost of on shrub.

Answer 1

The cost of 1 Rose Bush= $ 8

The cost of 1 Shrub = $12.

Explanation:

The cost of 11 rose bushes and 4 shrubs = $136

The cost of 2 rose bushes and 11 shrubs = $148

Let the cost of one rose bush = $x

and the cost of one shrub = $ y

Now, according to the question:

11 x + 4 y = 136

and 2 x + 11 y = 148

From (1), we get that 11x = 136 - 4y

or,
`x = (136 - 4y)/(11)`

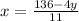
Substitute this value of x in equation (2), we get

`2 x + 11 y  = 148  \implies 2( (136 - 4y)/(11))  + 11y  = 148`

or,
`( (272 - 8y)/(11))  + 11y  = 148  \implies 272 - 8y + 121y = 1628`

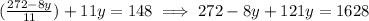
or, 113 y = 1356

or, y = 1356/113 = 12

⇒ y = 12, So
`x  =  (136 - 4y)/(11)  = (136 -12(4))/(11) = (136 - 48)/(11)  = 8`

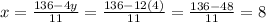
or, x =8 and y = 12 is the solution of the above system.

Hence, the cost of 1 rose bush = $x = $8

and The cost of 1 shrub = $ y = $12.