Question

Find the probability that you will roll an even number exactly 5 times when you: roll a six-sided number cube 10 times. P = 0.246 roll a six-sided number cube 20 times. P = 0.015 Explain why the second result is less.

Answer 1

Sample Response: As the number of trials changes, the distribution changes. Since there is a 50% chance of rolling an even number, having a small number of successes is less likely when the number of rolls increases.

The number of trials affects the distribution.

5 successes is the expected value for 10 trials.

5 successes is close to an end of the distribution for 20 trials.

Explanation:

Edge answer :)

Answer 2

Answer and explanation:

Given : The probability that you will roll an even number exactly 5 times when you: roll a six-sided number cube 10 times. P = 0.246 roll a six-sided number cube 20 times. P = 0.015

To find : Explain why the second result is less ?

Solution :

We have given that,

The probability that you will roll an even number exactly 5 times when we roll a six-sided number cube 10 times is P = 0.246.

Rolling a dice 10 times and get 5 times is
`(5)/(10)=0.5`

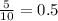
The probability that you will roll an even number exactly 5 times when we roll a six-sided number cube 20 times is P = 0.015.

Rolling a dice 20 times and get 5 times is
`(5)/(20)=0.25`

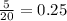
Since, the second result is less than first because 0.25 is less than 0.5 which means chances of 5 times in 20 times roll is less than 10 times.