Question

Pumps A, B, and C operate at their respective constant rates. Pumps A and B, operating simultaneously, can fill a certain tank in 6/5 hours; pumps A and C, operating simultaneously, can fill the tank in 3/2 hours; and pumps B and C, operating simultaneously, can fill the tank in 2 hours. How many hours does it take pumps A, B, and C, operating simultaneously, to fill the tank.

A. 1/3
B. 1/2
C. 1/4
D. 1
E. 5/6

Answer 1

Answer:D) 1 hr

Explanation:

Given

Pump A and B can fill tank in
`(6)/(5) hr`

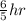
Pump A and C can fill tank in
`(3)/(2) hr`

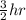
Pump B and C can fill tank in
`2 hr`

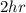
Let A be the total hr taken A therefore rate of
`A=(1)/(A) /hr`

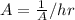
Let B be the total hr taken B therefore rate of
`B=(1)/(B) /hr`

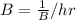
Let C be the total hr taken C therefore rate of
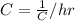
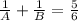`C=(1)/(C) /hr`

`(1)/(A)+(1)/(B)=(5)/(6)`-----1

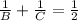`(1)/(B)+(1)/(C)=(1)/(2)`-----2

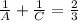`(1)/(A)+(1)/(C)=(2)/(3)`-----3

Adding 1,2 & 3

`2((1)/(A)+(1)/(B)+(1)/(C))=(5)/(6)+(1)/(2)+(2)/(3)`

`(1)/(A)+(1)/(B)+(1)/(C)=(2)/(2)`

`(1)/(A)+(1)/(B)+(1)/(C)=1`

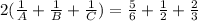
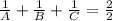
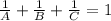
thus time taken by A,B and C combined is 1 hr