Answer:
The attached system shows that there’s an integrator between the point where disturbance enters the system and error measuring element. A any time when R(s)=0 then
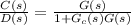 and considering that
and considering that
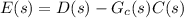 then
then

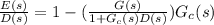
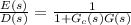

For ramp disturbance d(t)=at
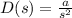 therefore, the steady state error is given by
therefore, the steady state error is given by
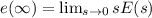
![e(\infty)= \lim_(s \to 0) s [\frac {D(s)}{1+G_c(s)G(s)}]](https://img.qammunity.org/2020/formulas/engineering/college/m5hxd82vetzco2w2xo88z13a81xjfltx0k.png)
![e(\infty)= \lim_(s \to 0) s [\frac {a}{s^(2)+s^(2)G_c(s)G(s)}]](https://img.qammunity.org/2020/formulas/engineering/college/kjcyul4h0p8zbucukjiaimny84dhdy4scl.png)
![e(\infty)= \lim_(s \to 0) s [\frac {a}{s+sG_c(s)G(s)}]](https://img.qammunity.org/2020/formulas/engineering/college/ycqh9i15u1phxwxhvgb809ms0vl8upvo51.png)
![e(\infty)= \lim_(s \to 0) s [\frac {a}{sG_c(s)G(s)}]](https://img.qammunity.org/2020/formulas/engineering/college/wxddfy4vjwnu1wk8qlm7t2x8vp6v2ib776.png)
Whenever
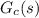 has a double intergrator, the error
has a double intergrator, the error
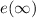 becomes zero
becomes zero