Answer:
Observe that f(x) is a continuous function when
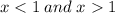 because is a polynomial. The possible problem may occur in x=1.
because is a polynomial. The possible problem may occur in x=1.
Then, f(x) is discontinuous in x=1 if the limits of f to the right and the left of 1 exist and are different or if some of those limits doesn't exist.
Let's calculate the limits:
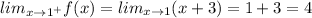
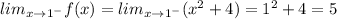
Since,
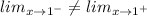 then f(x) is discontinuous in x=1.
then f(x) is discontinuous in x=1.