Question

Consider the equation 2x + 2y = 8.

Part A: Write an equivalent equation by multiplying the equation by 3.
Does the equation have the same solution set?
Part B: Write an equivalent equation by dividing the equation by 2. Does
the equation have the same solution set?

Answer 1

Part A) see the explanation

Part B) see the explanation

Explanation:

we have

`2x+2y=8`

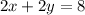
Part A) Write an equivalent equation by multiplying the equation by 3.

Does the equation have the same solution set?

Multiply by 3 both sides

`3(2x+2y)=3(8)`

`6x+6y=24`

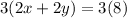
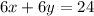
Remember that

The Multiplication Property of Equality states that if you multiply both sides of an equation by the same number, the sides remain equal

therefore

The equivalent equation have the same solution set by multiplication property of equality

Part B) Write an equivalent equation by dividing the equation by 2. Does

the equation have the same solution set?

Divide by 2 both sides

`(1/2)(2x+2y)=(1/2)(8)`

`x+y=4`

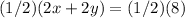
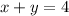
Remember that

The Division Property of Equality states that if you divide both sides of an equation by the same number, the sides remain equal

therefore

The equivalent equation have the same solution set by division property of equality