Question

A parcel delivery service will deliver a package only if the length plus girth (distance around) does not exceed 84 in. What are the radius, length and volume of the largest cylindrical package that may be sent using this service?

The radius of the largest cylindrical package is ? in
The length of the largest cylindrical package is ? in
The volume of the largest cylindrical package is ? in^3
(us pi as needed)

Answer 1

the answer above is correct except for the volume

Explanation:

The volume setup was correct, but the answer above forgot to square the radius, meaning the correct volume would be
`6987.54 in^(2)`

:)

Answer 2

a)
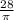`(28)/(\pi)` in

b) 28 in

c) 784 in²

Explanation:

Let the length be 'L'

and the radius be 'r'

Thus, according to the question

L + 2πr = 84 in

L = 84 - 2πr ............(1)

Volume of the cylinder, V = πr²L

substituting the value of L from 1, we get

V = πr²(84 - 2πr)

or

V = 84πr² - 2π²r³

for points of maxima, differentiating the above equation and equating it to zero

`(dV)/(dr)=(d(84\pi r^2-2\pi^2 r^3)))/(dr)`

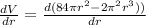
or

2(84)πr - 3(2)π²r² = 0

or

2πr(84 - 3πr) = 0

or

r = 0 and 84 - 3πr = 0

or

⇒ 3πr = 84

or

⇒ r =
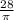`(28)/(\pi)` in

since, the radius cannot be zero therefore, r = 0 is neglected

Therefore,

a) The radius of the largest cylindrical package =
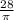`(28)/(\pi)` in

b) from (2)

L = 84 - 2πr

or

⇒ L =
`84 - 2\pi*(28)/(\pi)`

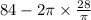
or

⇒ L = 84 - 56 = 28 in

The length of the largest cylindrical package = 28 in

c ) The volume of the largest cylindrical package ,V = πr²L

=
`\pi*(28)/(\pi)*28`

= 784 in²