Answer:
a)
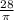 in
in
b) 28 in
c) 784 in²
Explanation:
Let the length be 'L'
and the radius be 'r'
Thus, according to the question
L + 2πr = 84 in
L = 84 - 2πr ............(1)
Volume of the cylinder, V = πr²L
substituting the value of L from 1, we get
V = πr²(84 - 2πr)
or
V = 84πr² - 2π²r³
for points of maxima, differentiating the above equation and equating it to zero
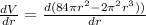
or
2(84)πr - 3(2)π²r² = 0
or
2πr(84 - 3πr) = 0
or
r = 0 and 84 - 3πr = 0
or
⇒ 3πr = 84
or
⇒ r =
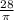 in
in
since, the radius cannot be zero therefore, r = 0 is neglected
Therefore,
a) The radius of the largest cylindrical package =
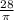 in
in
b) from (2)
L = 84 - 2πr
or
⇒ L =
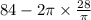
or
⇒ L = 84 - 56 = 28 in
The length of the largest cylindrical package = 28 in
c ) The volume of the largest cylindrical package ,V = πr²L
=
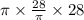
= 784 in²