Answer:
The measurement of arc BC is 130°.
Explanation:
Given : circle with origin O, with two line segments AC and BD which are also diameters.
Measurement of arc AB = (3 x -70)° =
Measurement of arc DC= (x +10)° = ∠3
To find : Measurement of arc BC = ∠2 =?
Solution:
Let angle subtended by the arc AC = ∠1 = (3 x -70)°
Let angle subtended by the arc BD = ∠2
Let angle subtended by the arc DC = ∠3 = ( x + 10)°
Let angle subtended by the arc AD = ∠4
AC and BD are intersecting each other at O.
So, ∠1 = ∠3 (vertically opposite angles)..[1]
∠2 = ∠4 (vertically opposite angles)..[2]
(3 x -70)° = (x +10)° (from [1])
3x - x = 10 + 70
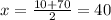
∠1 = ∠3 = (x +10)° = (40 +10)° = 50°
∠1 + ∠2 + ∠3 + ∠4 = 360°
50° + ∠2 + 50° + ∠2= 360° (from [2])
2∠2 = 360° -50° - 50°
2∠2 = 260°
∠2 = 260° ÷ 2
∠2 = 130°
The measurement of arc BC is 130°.