Question

A ball is initially dropped from rest from a height . It hits the floor and rebounds. It bounces several times before eventually coming to rest. Draw predictions for what graphs of the following quantities look like as functions of time. Include the first three bounces (i.e. the first three impacts with the floor)

(a) Height h(t)
(b) Magnitude of velocity [v(t)]
(c) Magnitude of acceleration [a(t)]

Answer 1

Step-by-step explanation:

We should start first with a(t), then plot v(t) and h(t)

a = g = -9.81 m/s2 is exerted by gravitational acceleration and constant no matter what t is. Since we are plotting only the magnitude, we can expect a straight horizontal line at 9.81.

`v(t) = v_0 + at = v_0 - 9.81t`

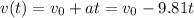
Since the ball start from rest,
`v_0 = 0 m/s`

`v(t) = -9.81t`

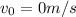
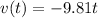
v(t) would start out negative, then increasing negatively in magnitude, as soon as the ball hit the floor and rebounds, expect the v jumps to positive value immediately after, then decrease in magnitude until 0 where it gets to maximum height.

The plot of v magnitude should be v-shaped.

As for height:

`h(t) = h_0 + vt + at^2/2`

`h(t) = h_0 + vt - 4.9t^2`

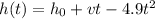
Since this is a quadratic equation, we can expect the plot to be parabolic-shaped.

Picture of graph is attached