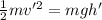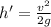Question

Two blocks are free to slide along a frictionless, wooden track. The track consists of a curve of height 5 m that falls to a straightaway. A smaller block weighing 5 kg is allowed to fall from the top the curve. It has a spring pointed forward embedded at the front. After reaching the straightaway, it collides with a larger block weighing 18 kg that is hard and flat at its rear. The two blocks rebound elastically. What is the final speed of the larger block? How high does the smaller block go back up the ramp?

Answer 1

Final speed is 8.506 m/s

Height of the block is 0.1 m

Solution:

As per the question:

Mass of the smaller block, m = 5 kg

Height of the track, h = 5 m

Mass of the larger block, M = 18 kg

Now,

To calculate the final speed of the larger block:

Consider that both the momentum and the energy of the block is conserved as the track is friction-less.

If the smaller block is at a height 'h' then it will have potential energy only.

The initial energy of the entire system is ;

`E_(i) = PE = mgh`

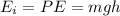
As it starts moving on the track, the potential energy is completely transfomed into Kinetic energy that provides motion, thus the final enrgy:

`E_(f) = KE = (1)/(2)mv^(2)`

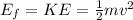
Following the conservation of energy:

`E_(i) = E_(f)`

`mgh = (1)/(2)mv^(2)`

`v = √(2gh)`

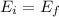
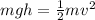
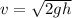
Since, the collision is elastic, both Kinetic energy of the blocks and the momentum are conserved.

Now,

Initial Momentum,
`p_(initial) = mv`

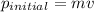
Final Momentum,
`p_(final) = -mv' + Mv''`

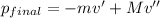
Now, by the conservation of momentum:

`p_(initial) = p_(final)`

`mv = -mv' + Mv''`

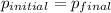
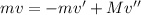
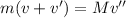`m(v + v') = Mv''` (1)

From the conservation of kinetic energy:

`(1)/(2)mv^(2) = (1)/(2)mv'^(2) + (M)/(v''^(2))`

`m(v^(2) - v'^(2)) = Mv''^(2)` (2)

Dividing eqn (1) and (2), we get:

v = v' + v''

Also, from above, we can write:

v' + v'' =
`√(2gh)`

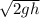
v' + v'' =
`√(2gh)`

v' =
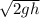
`√(2gh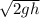)` - v'' (3)

Using eqn (3) in eqn (1) and (2) and solving we get:

`√(2gh)(2m)/(M + m)`

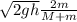
Using proper values in the above eqn:

`v'' = √(2* 9.8* )(2* 5)/(18 + 5) = 8.506\ m/s`

`v' = √(2* 9.8* 5) - 8.506 = 1.393\ m/s`

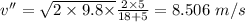
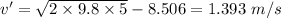
Now, the Kinetic energy required to climb the curve:

`E_(i) = (1)/(2)mv'^(2)`

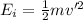
Now, at height h':

`E_(f) = mgh'`

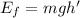
By the conservation of energy principle:

`(1)/(2)mv'^(2) = mgh'`

`h' = (v^(2))/(2g)`

`h' = (1.393^(2))/(2* 9.8) = 0.1 m`