Question

A firm is considering making a one-time investment of $12.0 million, payable in full today. It is expected this would increase the firm's free cash flows by $300,000 in one year, increasing by 3% each year thereafter, forever. So in two years, for example, this investment will result in $309,000 more cash for the firm. What is the IRR of this investment?

Answer 1

The IRR of this investment is 5.5%

Step-by-step explanation:

First we need to express the present value of this investment

`PV=-12+(0.3)/(1+r) +(0.3*1.03)/((1+r)^2)+(0.3*1.03^2)/((1+r)^3)+... +(0.3*1.03^(k-1))/((1+r)^k)`

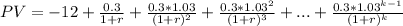
From the second term we have a perpetuity with growth rate, which we resolve as

`(0.3)/(1+r) +(0.3*1.03)/((1+r)^2)+(0.3*1.03^2)/((1+r)^3)+... +(0.3*1.03^(k-1))/((1+r)^k)=(0.3)/(r-0.03)`

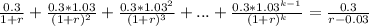
Then we can replace r by IRR and PV equal to zero and we have

`PV=0=-12+(0.3)/(IRR-0.03)\\ \\(0.3)/(IRR-0.03)=12\\\\IRR=0.03+0.3/12=0.03+0.025=0.055`

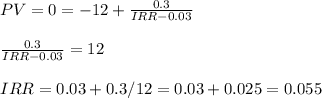
The IRR of this investment is 0.055 or 5.5%